Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

please help with trigo
The value of sin 5π/6 is 1/2, if you remember your special angle list. So, the question simplifies into finding the value of sin inverse of (-1/2).
We are finding a specific principal angle, θ, such that θ = sin inverse (-1/2). The principal range of sin inverse of a value is -π/2 ≤ θ ≤ π/2.
In other words, we are essentially solving the equation sin θ = -1/2, where -π/2 ≤ θ ≤ π/2. So, the angle we wish to look for is either in the fourth quadrant or the first quadrant. Since the right side value is negative, our required angle must be in the fourth quadrant.
The basic/reference angle to this is π/6, which is pretty much expected since we are taking the sine inverse of a sine.
The angle we wish to look for is a fourth , quadrant angle with basic angle π/6, or in short, -π/6.
You know what to do now.
See 1 Answer



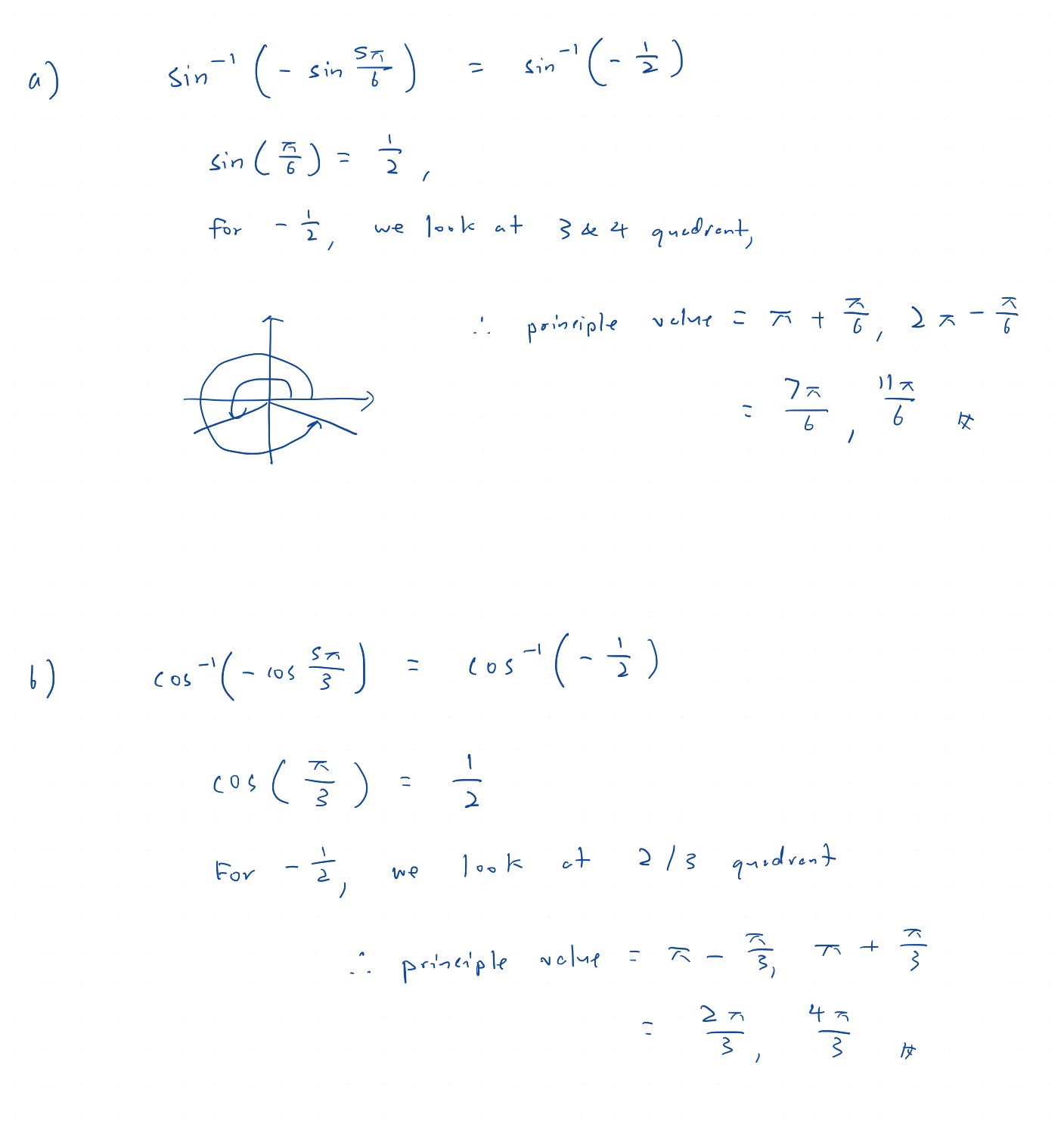


Correct for part (a) is -π/6, which is basically a fourth quadrant version of the basic reference angle π/6.
Do note that for part (b), the principal angles for arccos (inverse cos) are in the range 0° ≤ θ ≤ 180° in the case of degrees or 0 ≤ θ ≤ π in the case of radians.
Correct for part (b) is 2π/3, which is basically a second quadrant version of the basic reference angle π/3.