Because AQD and BQC are straight lines, angles AQP and DQR are equal, vertically opposite, angles.

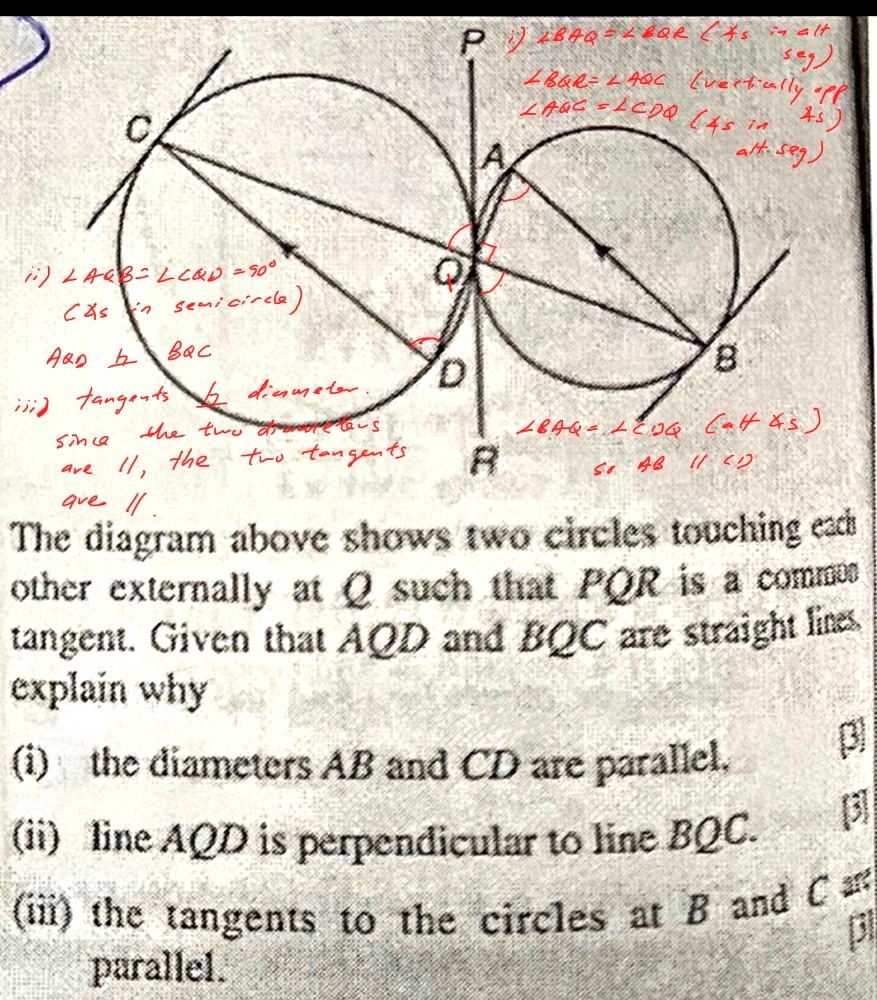
If PQR is a common tangent,
- AQP = ABQ (alternate segment / tangent-chord theorem)
- DQR = DCQ (alternate segment / tangent-chord theorem)

So, this means that ABQ = DCQ. But BQC is a straight line, so this necessitates that lines AB and CD are parallel due to the alternate angles property. So, from the converse of the alternate angles property, we can say that both lines AB and CD are parallel.

[Note that converse reasoning does not work for all scenarios (eg everyone 5 years of age are children, but not every children are 5 years of age), but for alternate angles it works both ways]

AB and CD are said to be diameters from part A.

CQD and AQB are both 90 degrees since they are angles in a semicircle.

Needless to say, CQA and BQD are also 90 degrees because AQD and BQC are straight lines.

So, AQD is perpendicular to BQC.

Since lines AB and CD are parallel, angle BAQ = angle CQD.

[In fact, we can use the same angle comparison for part (i) because you can find another set of angles satisfying the alternate segment / tangent-chord theorem]

But angle BAQ = angle QB(some point south-west of B along the tangent, let’s call it X)) and angle CQD = angle QC(some point north-east of C along the tangent, let’s call it Y) due to the alternate segment / tangent-chord theorem.

For both QBX and QCY to be equal, it is necessary that the two tangents are also parallel, by converse reasoning of the alternate angles property.

So, the two tangents are parallel.

Thks v much for the detailed explanation!