Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
primary 5 | Maths
| Fractions
2 Answers Below
Anyone can contribute an answer, even non-tutors.

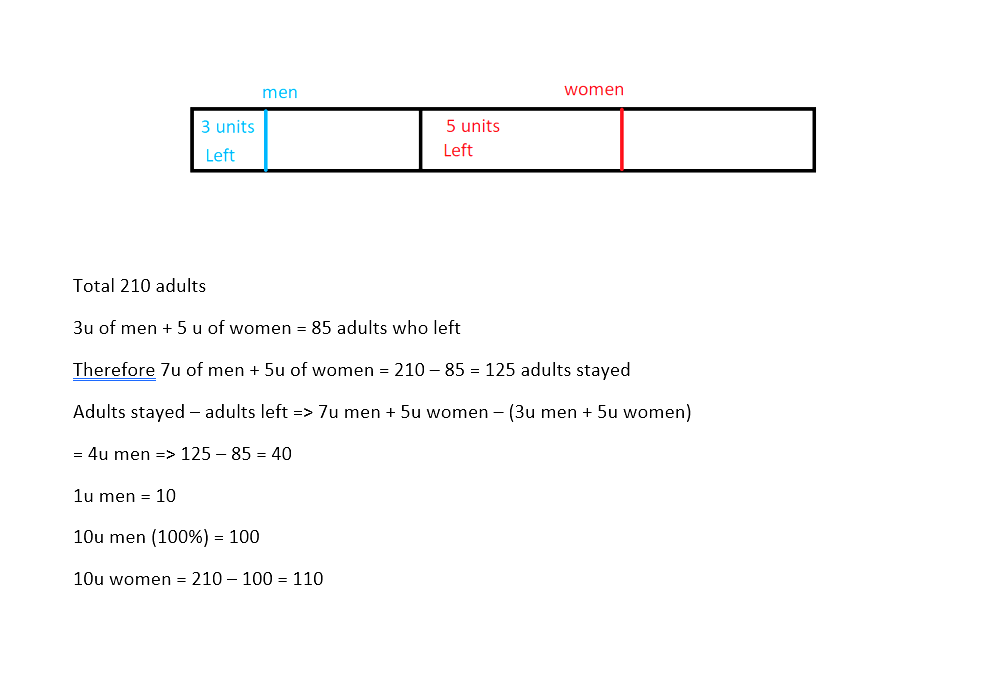
Women: 110
Men: 100
Was able to solve this algebraically. Was wondering if anyone knows how to do this via the “model method”
I regularly tell my students of the need to shift away from model ideas the moment they reach P6 level.
30% men left the ball
85 left the hall
Ok actually come to think of it, for this particular question model is entirely possible because 50% is quite a nice figure.
We can draw a model as follows.
50% of women and 30% of men = 85
50% of women and 70% of men = 125
x = 50% of women (so there are two “x” in total)
o = 10% of men (so there are ten “o” in total)
xooo
xooooooo
First one is for 85 people
Second one is for 125 people
oooo = 40 people
o = 10 people
10 “o” = 100 people
So we have 100 men and 110 women
Normally I try to use ratios in place of such models to try and explain my concepts. I always highlight the importance of “same quantities” and “multiplier quantities” in questions. For example, “there are the same number of boys and girls at first”. Or, “there are twice as many boys as girls at first”. Or something along that line.
Once there are too many quantities involved, especially those without multipliers, I would introduce the “unit-part” method to them - technically that’s an algebraic approach already by then.
Generally the stronger students are more willing to learn algebraic approaches as they are more confident of their skills and are willing to explore alternative approaches.
The weaker ones, on the other hand, will already find the algebraic questions in P6 very challenging as they struggle to grasp the manipulation of basic algebraic addition and subtraction.
Ratios become particularly important as techniques, while percentages can get confusing to them.
If your students are generally strong, you could hide the algebraic concepts as “units and parts”. Or, you would show them, in a model setting, how “x” is like “1 unit” when it comes to a model. You can then show them that the operations in algebra are akin to what they have already been doing.
See 2 Answers