Need to prove that EXO and EFB are also similar, though this is easy to prove.

We need to do some calculations.

Will type out later at ~ 2 am.

Ok, so here's the deal.

If HO would be parallel to FB, it would make things simpler. But nowhere in the question mentioned this.

I give you a hint: it's indeed parallel. But how do we show this? (It's a prelude to the Midpoint Theorem)

----------------------------------------------

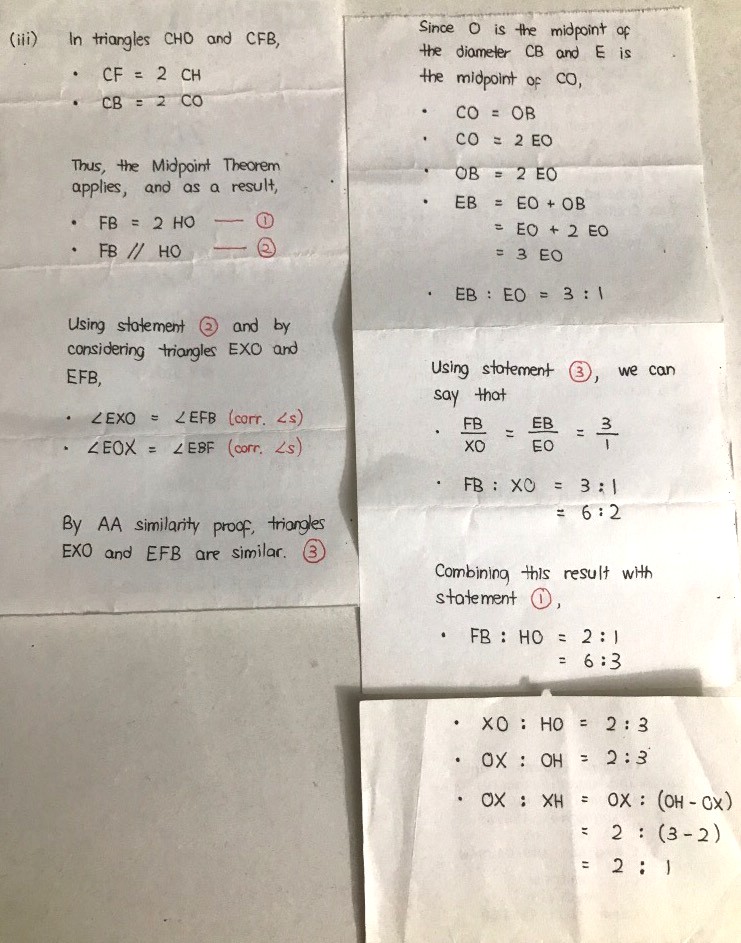
Consider triangles CHO and CFB.

• Notice clearly that CF = 2 CH because we are given that H is the midpoint of CF.

• Similarly, CB = 2 CO because O is the midpoint of the chord CB (meaning to say, both CO and OB are radii of the circle)

• So, the length ratio CF/CH = CB/CO = 2/1.

• With the sandwiched angle at C being a common angle, we have completed the S-A-S similarity proof.

------------------------------------------------

With the two triangles being similar, we will obtain the following result.

• Angle CHO = Angle CFB

But this would fall under the good corresponding angle rule - which can only happen when HO is parallel to FB.

[So, the converse of the corresponding angle rule will be true as well]

Now we will need this for our proof.

Will update this in the next post.

We have already proved that triangles CHO and CFB are similar.

The subsequent result HO // FB is just as important.

Looking at triangles EXO and EFB, we will see several instances of corresponding angles
• Angle EXO = Angle EFB [A]
• Angle EOX = Angle EBF [A]

[Needless to say, angle E is common]

This completes our A-A similarity proof for triangles EXO and EFB.

Now, it's time to do the calculations.

------------------------------------------------------

(First point)

First, what can we tell about the length ratio FB : HO?

Well, we have already found that triangles CFB and CHO are similar, with length ratio 2 : 1.

By default, FB : HO would also be 2 : 1.

------------------------------------------------------

(Second point)

Observe that O is the midpoint of CB and E is the midpoint of CO. This means that
• CB = 2 CO
• CO = 2 EO
• EO : OB = 1 : 2
• EO : EB = 1 : 3

So, the length ratio of the corresponding lengths in triangles EXO and EFB are always 1 : 3.

• XO : FB = 1 : 3

-------------------------------------------------------

(Final result)

Let's combine the overall results.

• FB : HO = 2 : 1 = 6 : 3
• XO : FB = 1 : 3 = 2 : 6

As we know it too well,
• XO : FB : HO = 2 : 6 : 3
• XO : HO = 2 : 3
• OX : OH = 2 : 3

Now, it's clear that

• OX : XH = 2 : (3 - 2) = 2 : 1