Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

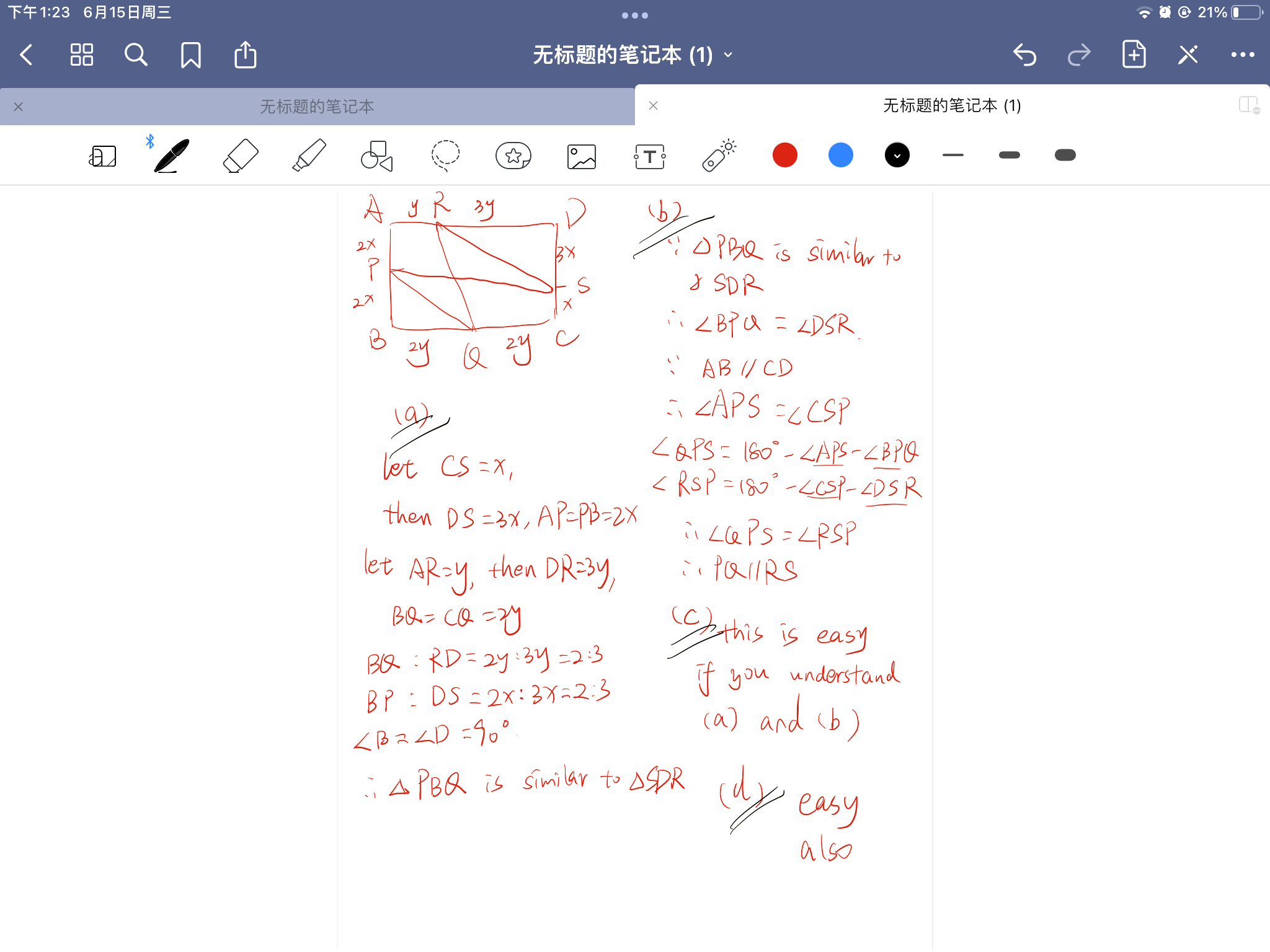
can someone help me with this question! I can’t seem to form the correct ratios for the values. I’m not quite sure how to form ratios correctly. Help would be greatly appreciated asap thank you!! <3
CS : CD = 1 : 3
[You could use units and parts if you prefer to, but it has been two and a half years since you last used units and parts, correct?]
Let the length of AD be 6x (i.e. "6 units") and the length of CD be 6y (i.e. "6 parts").
[Note that I used 6 and not 3 because I quickly noticed that I was supposed to divide the vertical widths of the rectangle into two or three equal portions - AB into two portions and DC into three portions]
Then, all of the following points hold true.
- AR = 2x
- RD = 4x
- BQ = 3x
- QC = 3x
- AP = 3y
- PB = 3y
- DS = 4y
- SC = 2y
Now, on to the proof. We cannot assume that PQ and RS are parallel as of now (we will eventually prove it later on), so we have to rely on length ratios.
- Two corresponding angles are equal (their third corresponding angle will be automatically equal)
- Three corresponding sides are of the same ratio
- Two corresponding sides are of the same ratio AND their sandwiched angles are equal
We will use the third approach for this question.
We know that angles PBQ and SDR are 90 degrees since they are vertices of rectangle ABCD.
==> angle PBQ = angle SDR [Angle}
These angles are sandwiched between lengths PB and BQ (for angle PBQ) and lengths SD and DR (for angle SDR).
We see that
- PB/SD = 3y/4y = 3/4
- BQ/DR = 3x/4x = 3/4
and so it follows that PB/SD = BQ/DR. This is what is meant by "the corresponding sides are in the same ratio". The ratio here is 3 : 4.
==> PB/SD = BQ/DR [Side Ratio]
These two points are sufficient for the similarity proof. We have used the Side-Angle-Side [SAS] proof for our similarity. Note that this is distinct from the Side-Angle-Side [SAS} proof for congruency as the corresponding sides would have to be equal.
So, triangles PBQ and SDR are similar.
Now that both triangles are similar, let's prove that PQ is parallel to RS.
From the similarity proof, we can conclude that angles PQB and SRD are equal. This means that lines PQ and SR are inclined to horizontal lines BC and DA respectively at equal angles. This is sufficient to prove that PQ is parallel to RS.
Alternatively, you can use gradient ideas to show this, by considering that gradient of PQ = gradient of RS = -y/x. I will leave this to you to think through what this means.
We have figured that PQ and RS are parallel lines. This is pivotal in solving part c.
Remember what I mentioned earlier on? We can prove that two triangles are similar in these ways.
- Two corresponding angles are equal (their third corresponding angle will be automatically equal)
- Three corresponding sides are of the same ratio
- Two corresponding sides are of the same ratio AND their sandwiched angles are equal
We will use the first approach for this question (the Angle-Angle proof).
Well, you would have guessed it right - angles PQT and SRT are equal as they are alternate angles. How about angles QPT and RST?
We can also consider the fact that angles PTQ and STR are vertically opposite angles.
We can use any two of the three arguments above to conclude that triangles PTQ and STR are similar.
One more part to go!
If triangles PTQ and STR are similar, then all their dimensions will be in that ratio. This also includes the ratio of their perpendicular heights!
As such the area ratio of both triangles will be the square of their length ratio - simply because area is a two-dimensional quantity!
But what are their length ratios then?
Recall that from part a, triangles PBQ and SDR are similar. Their length ratio must be 3 : 4 since the ratio of the length of PB to the length of SD is 3 : 4. This extends to PQ : SR as well!
So, PQ : SR = 3 : 4.
These two lengths are part of the two triangles in part c as well! So, the length ratio of the two triangles in part C would be 3 : 4.
Their perpendicular height ratios would also be 3 : 4. As such, we can simply say that the area ratio of both triangles is 3² : 4², or 9 : 16.
Since the area of triangle PTQ is 63 cm², then using our ratio 9 : 16, we can guess the area of triangle STR which is going to be...
...112 cm².
See 1 Answer
so PB = y/2, BQ = x/2,
in this case, SD = 3y/4, DR = 3x/4,
I do not like his method because it involved a lot of fractions and seemed not easy to understand.
But his idea is the same as mine.
It's AR : AD (rather than AR : RD) which is 1 : 3.
A similar argument ensues for CS : CD.
[RD takes up 2/3 of the length of AD while SD takes up 2/3 of the length of CD]