Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
junior college 1 | H2 Maths
3 Answers Below
Anyone can contribute an answer, even non-tutors.
Hi Mr Eric, I am stuck with another H2 Maths question. Could you kindly help me please? Thank you so much!
Date Posted: 2 years ago
Views: 529
See 3 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Good afternoon Candice! I found that the question's missing bracketing poses a challenge as to where the brackets could be.
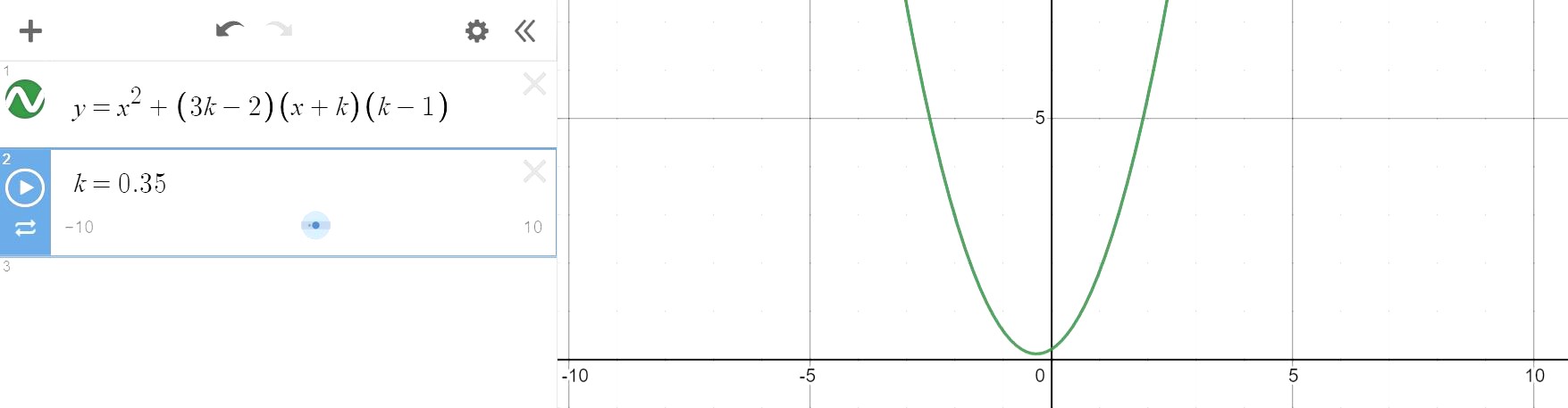
I found that for y = x² + (3k - 2) (x + k) (x - 1), the graph can have no real root as is the case shown here.
This is because I obtained my discriminant of roots as
D = (3k - 2) (k - 1) times [(3k - 2) (k - 1) - 4k] and I found that there was no way I could combine them, and upon inspection, indeed I could not prove the "always real roots" case.
Instead, I tried a different bracketing arrangement y = x² + (3k - 2) x + k(k - 1) and found that on Desmos, the graph always has two real roots! Will work my answers based on this later.
I found that for y = x² + (3k - 2) (x + k) (x - 1), the graph can have no real root as is the case shown here.
This is because I obtained my discriminant of roots as
D = (3k - 2) (k - 1) times [(3k - 2) (k - 1) - 4k] and I found that there was no way I could combine them, and upon inspection, indeed I could not prove the "always real roots" case.
Instead, I tried a different bracketing arrangement y = x² + (3k - 2) x + k(k - 1) and found that on Desmos, the graph always has two real roots! Will work my answers based on this later.
Date Posted:
2 years ago
Thanks Mr Eric !
Totally agreed with your findings :)
Totally agreed with your findings :)
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Good afternoon Candice! Here are my workings for the proving part and part (i).
Date Posted:
2 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Good afternoon Candice! Here are my workings for part (ii).
The fact that 3k - 2 = 0 goes to show that for quadratic curves which have their turning points at the y-axis itself, the line of symmetry must be the y-axis itself, so the coefficient of x has to be zero.
The fact that 3k - 2 = 0 goes to show that for quadratic curves which have their turning points at the y-axis itself, the line of symmetry must be the y-axis itself, so the coefficient of x has to be zero.
Date Posted:
2 years ago
Yes, I got it now :)
Thank you very much, Mr Eric!
Thank you very much, Mr Eric!
360 Tutoring Program