We can also solve this inequality without the substitution y = |x + 1|.

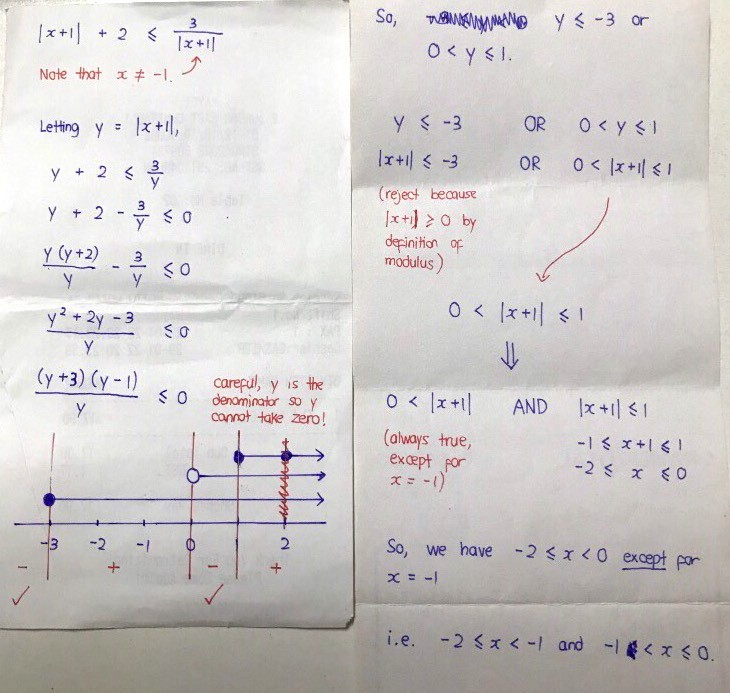
Notice that |x + 1| is always non-negative (can be zero or otherwise positive), but for this question, we cannot accept |x + 1| = 0 because there is the term |x + 1| in the denominator.

So, apart from the zero case, |x + 1| is otherwise always positive, so we can simply cross-multiply the denominator over.

[We should not cross-multiply expressions if the denominator cannot be established to be certainly positive or certainly negative]

Cross-multiplying,
|x + 1|² + 2 |x + 1| ≤ 3
|x + 1|² + 2 |x + 1| - 3 ≤ 0

This is a quadratic-like inequality which we can factorise like regular algebraic terms.

(|x + 1| + 3) (|x + 1| - 1) ≤ 0

So, we have

|x + 1| + 3 ≤ 0
OR
|x + 1| - 1 ≤ 0

The first scenario is not possible because |x + 1| + 3 is going to be a positive number. This leaves us with the second scenario.

|x + 1| - 1 ≤ 0
|x + 1| ≤ 1

Breaking up the inequality,
-1 ≤ x + 1 ≤ 1

Subtracting 1 from all sides gives
-2 ≤ x ≤ 0

But let's not forget that x cannot take a value of -1 due to the denominator present in the original inequality question.

So, -2 ≤ x < -1 or -1 < x ≤ 0.