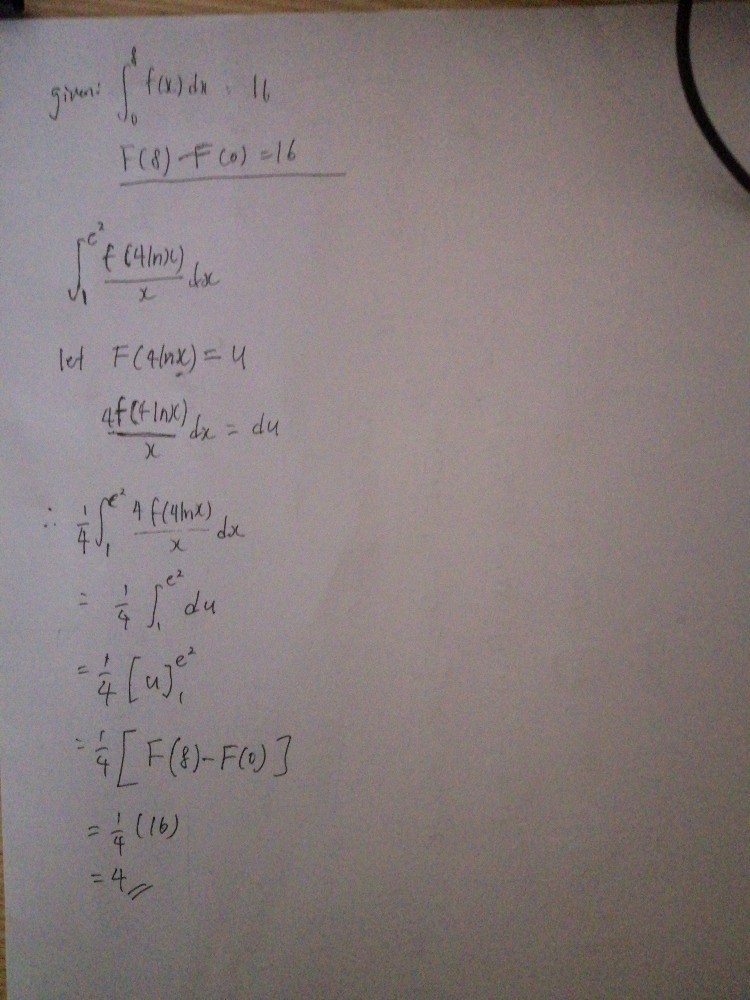Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
junior college 2 | H2 Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.
Does anyone knows how to get the value of 4?
Date Posted: 3 years ago
Views: 591
Explanation :
Let g(x) = ∫ f(x) dx
Then g'(x) = f(x)
For g(4ln(x)) , apply chain rule.
g'(4ln(x)) = f(4ln(x)) · d/dx (4ln(x))
= f(4ln(x)) · (4/x)
= 4 f(4ln(x)) / x
So,
∫₁ᵉ² f(4ln(x)) / x dx
= ¼ ∫₁ᵉ² 4 f(4ln(x)) / x dx
= ¼ [g(4ln(x))]₁ᵉ²
= ¼ [ g(4ln(e²)) - g(4ln(1)) ]
= ¼ [ g(8) - g(0) ]
= ¼ ∫₀⁸ f(x) dx
= ¼ (16)
= 4
Let g(x) = ∫ f(x) dx
Then g'(x) = f(x)
For g(4ln(x)) , apply chain rule.
g'(4ln(x)) = f(4ln(x)) · d/dx (4ln(x))
= f(4ln(x)) · (4/x)
= 4 f(4ln(x)) / x
So,
∫₁ᵉ² f(4ln(x)) / x dx
= ¼ ∫₁ᵉ² 4 f(4ln(x)) / x dx
= ¼ [g(4ln(x))]₁ᵉ²
= ¼ [ g(4ln(e²)) - g(4ln(1)) ]
= ¼ [ g(8) - g(0) ]
= ¼ ∫₀⁸ f(x) dx
= ¼ (16)
= 4
Alternatively,
∫₁ᵉ² f(4ln(x)) / x dx
= ¼ ∫₁ᵉ² f(4ln(x)) · 4/x dx
= ¼ [F(4ln(x))]₁ᵉ²
= ¼ [F(4ln(e²)) - F(4ln(1))]
= ¼ [F(8) - F(0)]
= ¼ ∫₀⁸ f(x) dx
= ¼ (16)
= 4
∫₁ᵉ² f(4ln(x)) / x dx
= ¼ ∫₁ᵉ² f(4ln(x)) · 4/x dx
= ¼ [F(4ln(x))]₁ᵉ²
= ¼ [F(4ln(e²)) - F(4ln(1))]
= ¼ [F(8) - F(0)]
= ¼ ∫₀⁸ f(x) dx
= ¼ (16)
= 4
See 2 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Hope this helps
Date Posted:
3 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
This idea can be considered.
Date Posted:
3 years ago
360 Tutoring Program