Relax relax. Desmos.com to the rescue.

I used Desmos too. But the thing is I don't know how to figure out on how to find the area.

I will explain that in a while. No worry

Thank you for frequently responding to my qns here!

First part :

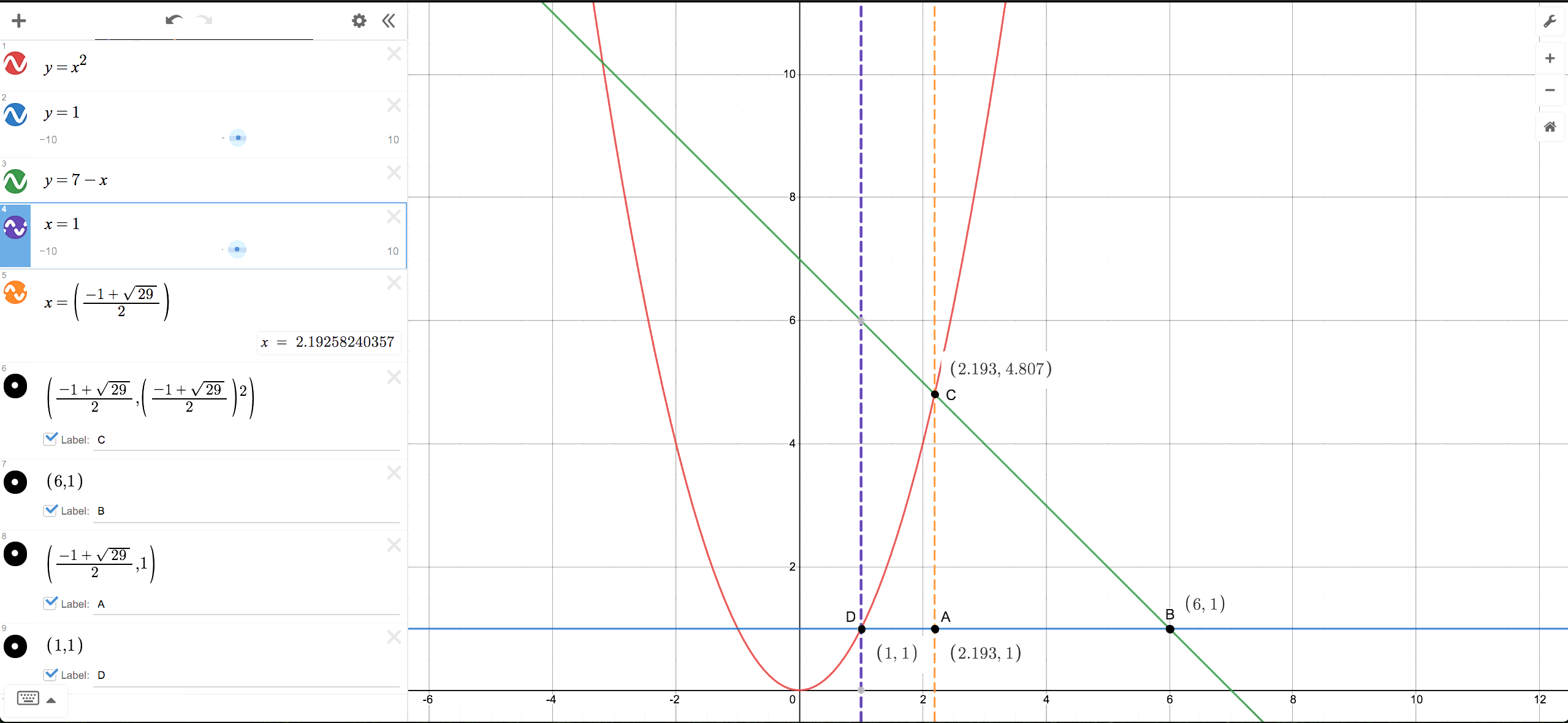
Find the intersection points of the curve and the lines.

When y = 1 and y = x²,

x² = 1
x = ±√1
x = 1 or x = -1

So the intersection point has coordinates (1,1)

When y = 7 - x and y = 1,

7 - x = 1
7 - 1 = x
x = 6

So the intersection point has coordinates (6,1)


When y = 7 - x and y = x²

7 - x = x²
x² + x - 7 = 0

Using the quadratic formula x = (-b±√(b²-4ac)) / 2a ,

x = (-1±√(1² - 4(1)(-7)) ) / 2(1)
x = (-1±√29) / 2)

x ≈ 2.193

(Edit : I decided to use the truncated 4s.f value for the rest of the calculations and workings for convenience and clarity)

So y ≈ (2.193)² ≈ 4.807


So the intersection point has coordinates (2.193,4.807)


We look at the graph (refer to the one I posted) and we notice that the bounded area is CBD.

We realise that the area consists of two parts, ABC and ADC.

ABC is a right angled triangle so we can simply use the formula ½ × base × height.
(AC is vertical and AB is horizontal)


ADC is bounded by the line x = 2.193 and the curve. We can integrate it, and then subtract the area of the rectangle formed by joining point D, A, and the intersection points of the x-axis and the lines x = 1 and x = 2.193.

Second part :

Area of △ ABC

= ½ × AB × AC

≈ ½ × (6 - 2.193) units × (4.807 - 1) units

≈ ½ × 3.807 units × 3.807 units

≈ 7.247 square units

(We also realise that △ABC is isosceles. The line y = 7 - x has gradient -1 so this means that the rise is just the negative of the run)



Area ADC

= ∫₁²·¹⁹³ x² dx - area of rectangle (length × breadth)

= [⅓x³]₁²·¹⁹³ square units - (2.193 - 1)units × (1 - 0)units

= (⅓(2.193)³ - ⅓(1)³) square units - 1.193 square units

≈ 1.989 square units


Total bounded area

≈ 7.247 square units + 1.989 square units

= 9.236 square units

If the exact value -1±√29 / 2 was used, you'll be getting approx 9.23585171609 for the final answer.

The answer derived from using the truncated x-value (x ≈ 2.193) is pretty close.


Alternatively, what you may choose to do is,

you can save the exact value in your scientific calculator and use it for all those calculations.

But you can write the 4s.f (or 5s.f) value for your workings on the answer booklet.

The final answer will be more accurate as compared to actually applying the truncated value in the calculator.

So long... thanks.

Welcome