Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 2 | H2 Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

Probability Qn. I need help with part (iii)!
Ans are
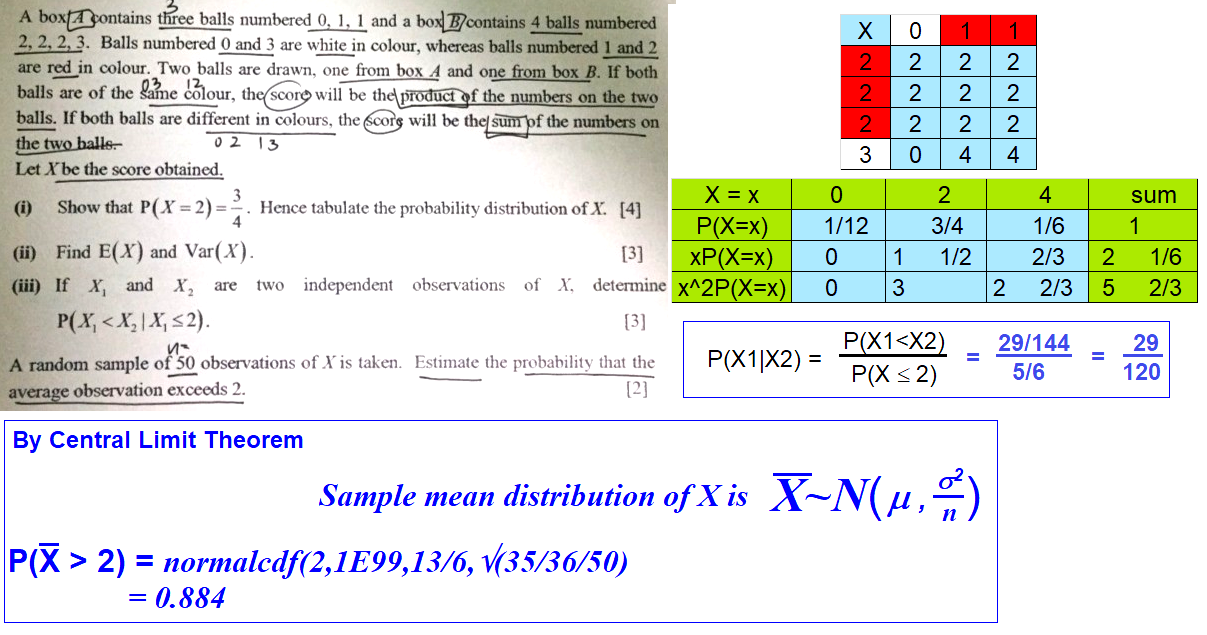
(i) P(X=0) = 1/12, P(X=1) = 0, P(X=2) = 3/4, P(X=3) = 0, P(X=4) = 1/6
(ii)13/6, 35/36
(iii)29/120, 0.884
P(X₁ = A and X₂ = B) = P(X₁ = A) × P(X₂ = B)
Then,
P(X₁ < X₂ ∣ X₁ ≤ 2)
= P(X₁ ≤ 2 and X₁ < X₂) ÷ P(X₁ ≤ 2)
= [P(X₁ = 2 and X₂ = 3)
+ P(X₁ = 2 and X₂ = 4)
+ P(X₁ = 1 and X₂ = 2)
+ P(X₁ = 1 and X₂ = 3)
+ P(X₁ = 1 and X₂ = 4)
+ P(X₁ = 0 and X₂ = 1)
+ P(X₁ = 0 and X₂ = 2)
+ P(X₁ = 0 and X₂ = 3)
+ P(X₁ = 0 and X₂ = 4) ]
÷ [P(X₁ = 0) + P(X₁ = 1) + P(X₁ = 2)]
= [ ¾ × 0
+ ¾ × 1/6
+ 0 × ¾
+ 0 × 0
+ 0 × 1/6
+ 1/12 × 0
+ 1/12 × ¾
+ 1/12 × 0
+ 1/12 × 1/6]
÷ [1/12 + 0 + ¾]
= [⅛ + 1/16 + 1/72] ÷ 5/6
= 29/144 × 6/5
= 29/24 × 1/5
= 29/120
P(X₁ ≤ 2 and X₁ < X₂) ÷ P(X₁ ≤ 2)
= [P(X₁ ≤ 2) - P(X₁ ≤ 2 and X₁ ≥ X₂)] ÷ P(X₁ ≤ 2)
= [P(X₁ = 0 + P(X₁ = 1) + P(X₁ = 2)
- P(X₁ = 0) × P(X₂ = 0)
- P(X₁ = 1) × P(X₂ = 0)
- P(X₁ = 1) × P(X₂ = 1)
- P(X₁ = 2) × P(X₂ = 0)
- P(X₁ = 2) × P(X₂ = 1)
- P(X₁ = 2) × P(X₂ = 2)]
÷ [P(X₁ = 0 + P(X₁ = 1) + P(X₁ = 2)]
= [1/12 + 0 + ¾
- 1/12 × 1/12
- 0 × 1/12
- 0 × 0
- ¾ × 1/12
- ¾ × 0
- ¾ × ¾]
÷ [1/12 + 0 + ¾]
= [5/6 - 1/144 - 1/16 - 9/16] ÷ 5/6
= 29/144 × 6/5
= 29/24 × 1/5
= 29/120
If the average exceeds 2, the total of 50 observations exceeds (2 × 50) = 100
What we want to do is to sum up all the variances Var(X) and expected values E(X) of all 50 independent observations first.
Let Y = X1 + X2 + X3 + ... + X50
Since they are all independent,
E(Y) = E(X1) + E(X2) + E(X3) + ... E(X50)
= 50 E(X)
= 50 × 13/6
= 108 ⅓
Var(Y) = Var(X1) + Var(X2) + Var(X3) +... + Var(X50)
= 50 Var(X)
= 50 × 35/36
= 48 11/18
Assume the total score of 50 observations is normally distributed.
So we can say :
Y ~ N(108⅓,√(48 11/18))
Then, find P(Y > 100) using your GC
normalcdf (100,200,108⅓√(48 11/18))
≈ 0.884001
= 0.884 (3s.f)
(Lower bound is 100, upper bound is 200 because the maximum total is 4 points per observation x 50 observations = 200)
Or,
find 1 - P(Y< 100)
1 - normalcdf (0,100,108⅓√(48 11/18))
≈ 1 - 0.115999
≈ 0.884001
= 0.884 (3s.f)
Define X̄ to be the average score of all the observations.
μ = E(X) = 13/6 = 2 1/6
σ = √Var(X)/√n
= √35/36 / √ 50
= √7/360
Then,
X̄~N(2 1/6, √7/360)
Probability that the average observation exceeds 2
= P(X̄ > 2)
normalcdf(2,4,2 1/6, √7/360)
(Upper bound here is 4 since the max average score is 4)
≈ 0.884001
= 0.884 (3s.f)
Using CLT, don't need as you mentioned.
On second look, fhe first case can use CLT directly already.
That means all those 50 observations i.e sample mean.
There was no mention of population mean.
'all the observations' ≠ 'every single possible 'observation' ≠ 'all observations' ≠ 'all possible scores observed'
There isn't actually a population here too anyway.
But the highest possible mean/average is only 4.
So not sure how the teacher/marker would grade that.
Did I say 'continuity correction is ONLY used for binomial distribution?'
I didn't.
So what misconception are you referring to?
No. And neither did I imply that... So what are you onto actually ? What is your concern?
http://jc-math.com/gce-a-level-h2-math/statistics/central-limit-theorem-eggs
The example in this website uses 'mean mass of 60 randomly chosen size 1 eggs'
Is this considered wrong to you then?
What is the appropriate phrasing in your opinion ?
Isn't that mean of all those 60 randomly chosen ones?
If not those 60, then which 60?
This 60? That 60? are you implying that the word 'any' should be used?
'all the observations' does not equal to 'all observations'
i.e it is not 'all possible observations'
Marks will not be lost and there is no strict or specific requirement that states that you must first state this :
X̄~N (μ,σ²/n)
You should also be aware of the different styles of presentation for the above.
Some styles go with stating the variance in the brackets, others state the S.D.
We can't say either is wrong. There's no fixed convention here. What is important is that it is clarified.
I can also say your workings are too short and you skip steps... risking loss of marks...
I see you have answered plenty of questions, but your profile is not listed.
See 2 Answers