a = 0, b = 8


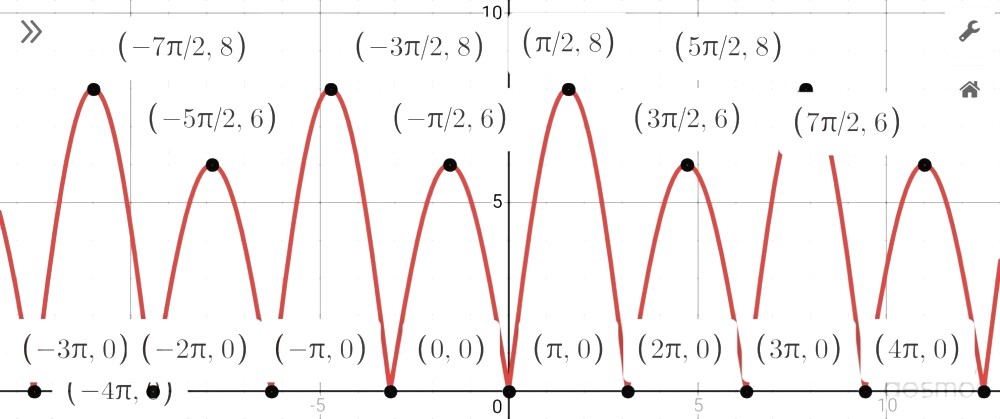
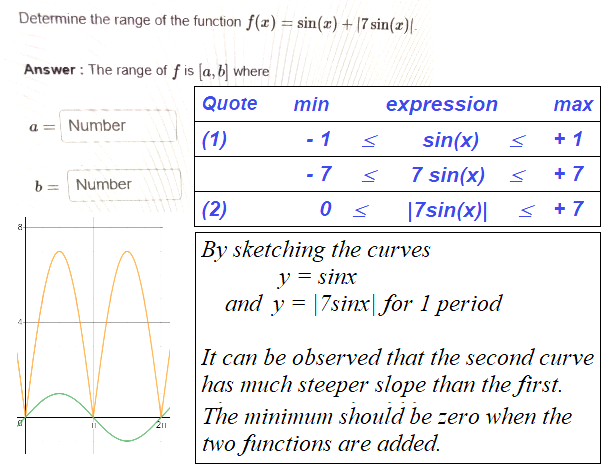
When sin(x) is at its lowest at -1,

|7 sin(x)|= |7(-1)| = |-7| = 7


Then sin(x) + |7 sin(x)| = -1 + 7 = 6


The minimum is at 0, when sin(x) = 0 and |7 sin(x)| = |7(0)| = 0

The maximum is at 8, when sin(x) = 1 and |7 sin(x)| = |7(1)| = 7

Here's how we can do it :


When sin(x) > 0,

f(x) = sin(x) + |7 sin(x)| = sin(x) + 7 sin(x) = 8 sin(x)

The modulus doesn't change the value here since sin(x) is already positive. So we can remove it and simply add the terms together.

sin(x) > 0 for the alternating domains 0 < x < π, 2π < x < 3π, 4π < x < 5π, etc.

So draw the function f(x) = 8 sin(x) for these domains/intervals.


When sin(x) < 0,

f(x) = sin(x) +|7 sin(x)| = sin(x) - 7 sin(x) = -6 sin(x)

Why?

sin(x) is negative means 7 sin(x) is negative too.

So the modulus sign will make 7 sin(x) a positive value. But if we need to write this positive value without the sign,

we will rewrite |7 sin(x)| as -7 sin(x) , such that the negative sign will negate the negative value of 7 sin(x), and turn it positive.


Eg. If sin(x) = -1, then |7 sin(x)| = |7(-1)| = |-7| = 7

Rewriting it as -7 sin(x) will immediately yield -7(-1) = 7

We do this so that we can add the terms together.


sin(x) < 0 for the alternating domains π < x < 2π, 3π < x < 4π, 5π < x < 6π, etc.

So draw the function f(x) = -6sin(x) for these domains/intervals.


As for sin(x) = 0,

these are the nodes where the function cuts the x-axis. They start from x = 0 and occur every π radians.