The graph y = x² + bx + c cuts the x-axis (horizontal line y = 0) at two points (-3, 0) and (2, 0).

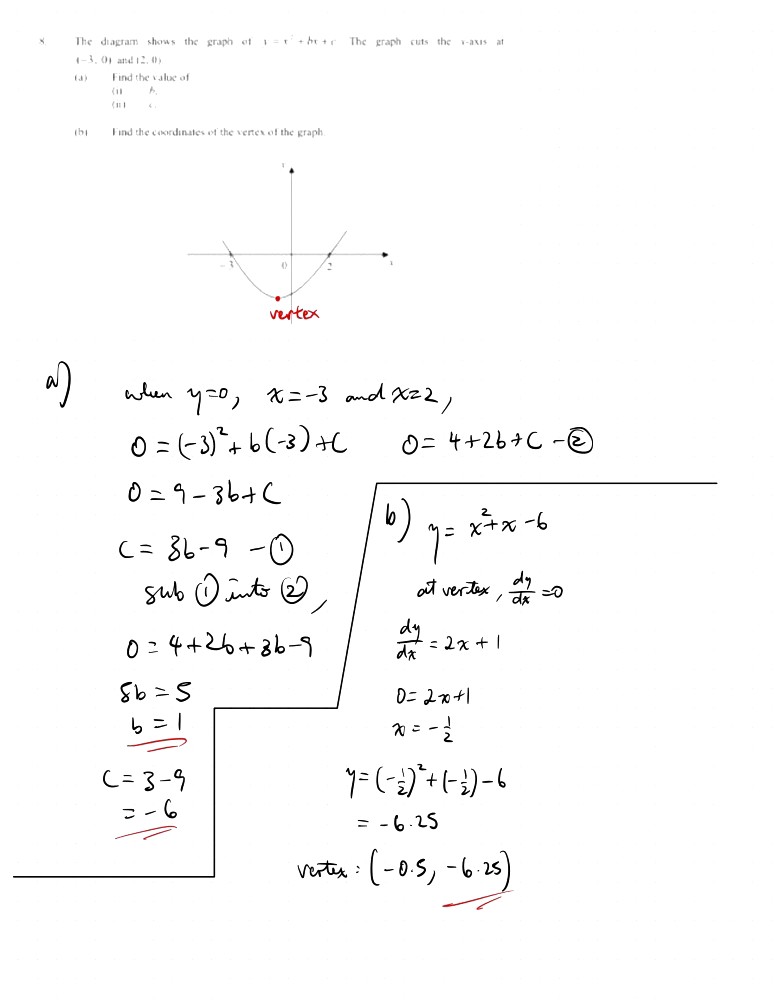
y = x² + bx + c (curve)
y = 0 (horizontal line which is the x-axis)

At the points where the the curve cuts the line, the y-values of both equations are identical so we can put the two equations simultaneously and the resulting equation becomes

x² + bx + c = 0.

The two points (-3, 0) and (2, 0) indicate that when y = 0, x can take the values -3 or 2.

So, the solutions to the equation x² + bx + c = 0 are -3 or 2.

We work this in reverse now.

x = -3 or x = 2
x + 3 = 0 or x - 2 = 0
(x + 3) (x - 2) = 0
x² - 2x + 3x - 6 = 0
x² + x - 6 = 0

The above steps, if you pay close attention, resemble the solving of a quadratic equation. It is the case, except that we are doing the steps in reverse because we would like to obtain the quadratic equation which gives us the said solutions.

This takes the form x² + bx + c = 0 where b = 1 and c = -6.

So, the original curve is y = x² + x - 6, with b = 1 and c = -6.

y = (x + 3) (x - 2)

The quadratic curve is well known for its vertical line of symmetry which passes through the turning point. Of course, even the points (-3, 0) and (2, 0) are symmetrical along this vertical mirror, so the x-value of this vertical mirror must be the average of -3 and 2, which is basically -1/2.

When x = -1/2,
y = (-1/2)² + 1/2 - 6
y = 1/4 + 1/2 - 6
y = -21/4

So, the vertex of the graph is (-1/2, -21/4).

I think that for a quadratic graph, "vertex" is not as accurate as "turning point".