Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | A Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

need help with this qn, pls explain too
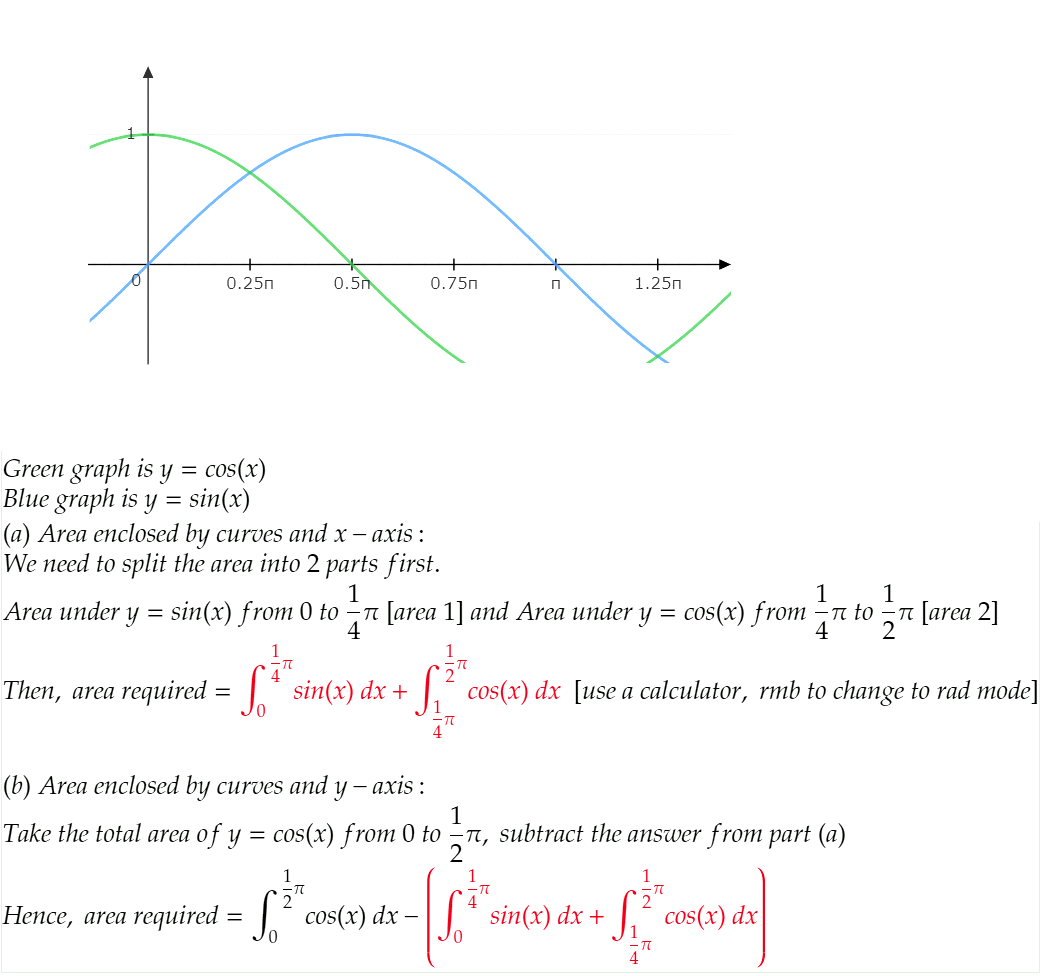
The two graphs will intersect at a point defined by
sin x = cos x
sin x / cos x = 1
tan x = 1
We will look at the lowest positive value of x (because the intersection they want is within 0 and pi/2)
x = pi/4
Housing the region x = 0 to x = pi/4 is the curve y = sin x and housing the region x = pi/4 to x = pi/2
Then, area housed by the first region
= INT sin x dx (upper limit pi/4, lower limit 0)
= [-cos x] upper lower
= - cos pi/4 - (-cos 0)
= - (sqrt2) / 2 + 1
Area housed by the second region
= INT cos x dx (upper limit pi/2, lower limit pi/4)
= [sin x] upper lower
= sin pi/2 - sin pi/4
= 1 - (sqrt 2) / 2
Their total area is 2 - sqrt 2.
I let you try the second part first
-x² + 5x + 4 = 8
-x² + 5x - 4 = 0
x² - 5x + 4 = 0
(x - 1) (x - 4) = 0
x = 1 or x = 4
You need this later on, and you will need to realise that y = -x² + 5x + 4 is a sad face graph which will cut the line y = 8 twice, at x = 1 (when the curve is going up) and at x = 4 (when the curve is going down)
See 2 Answers
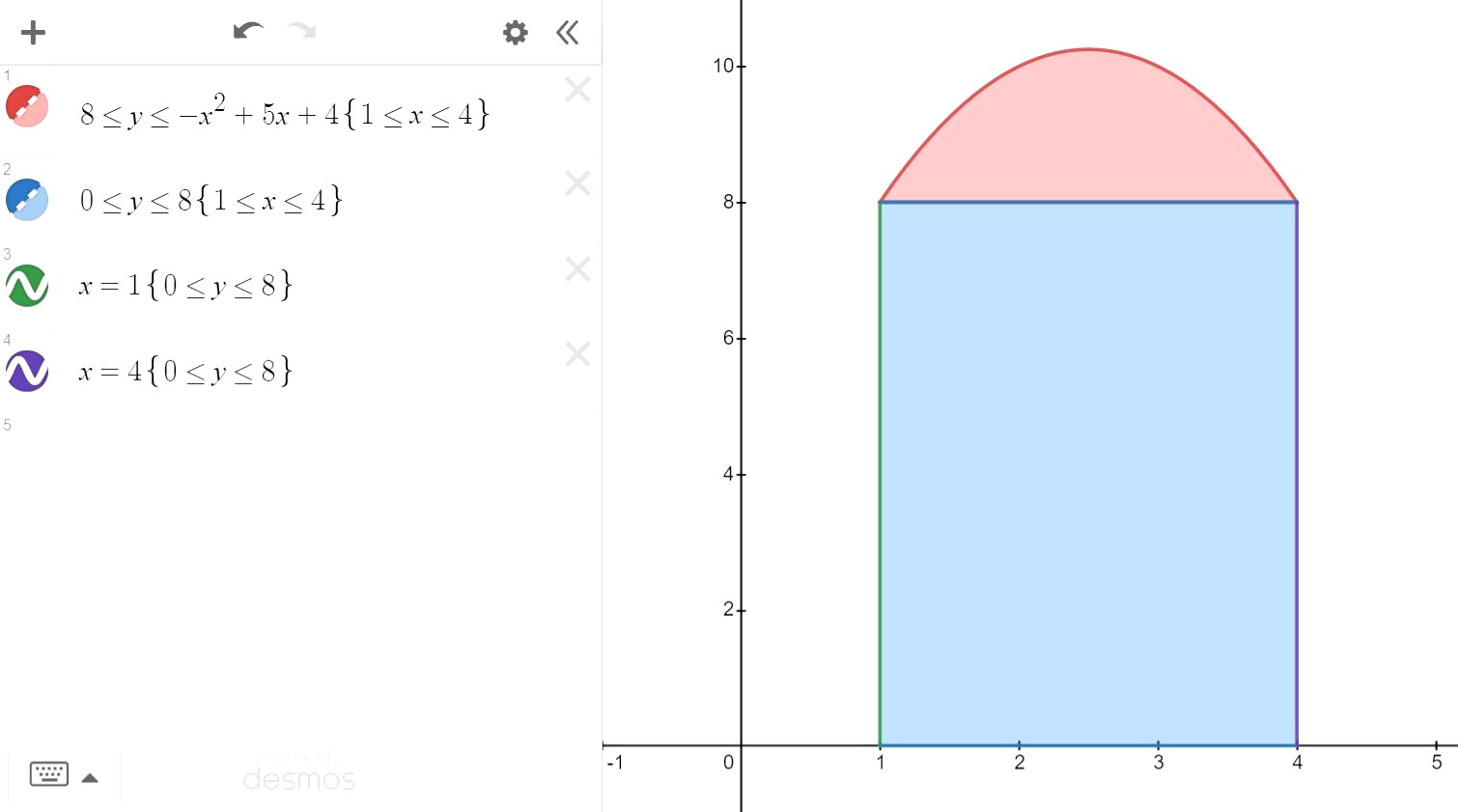
The area of the region we want is basically the area of the red region in the picture (which is enclosed by the curve and the horizontal line).
The red region is not touching the x-axis directly, so we cannot just take the area under the curve, since the area under the curve from x = 1 to x = 4 is the entire shaded region of both the red and the blue regions (under the curve ONTO the x-axis).
The area which we are looking
= Area under curve - Blue rectangle
= INT (-x² + 5x + 4) dx [upper is x = 4, lower is x = 1] - [3 x 8]
= [-x³/3 + 5x²/2 + 4x] [upper is x = 4, lower is x = 1] - 24
= [-4³/3 + 5 (4)²/2 + 4 (4)] - [-1³/3 + 5 (1)²/2 + 4 (1)] - 24
= [-64/3 + 40 + 16] - [-1/3 + 5/2 + 4] - 24
= 104/3 - 37/6 - 24
= 9/2 units²