Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | E Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

[Parabolas and Circles Basic Question]
The picture shown is ans. However i still don't understand the steps. Especially the equation after "Therefore".
*This is the question*
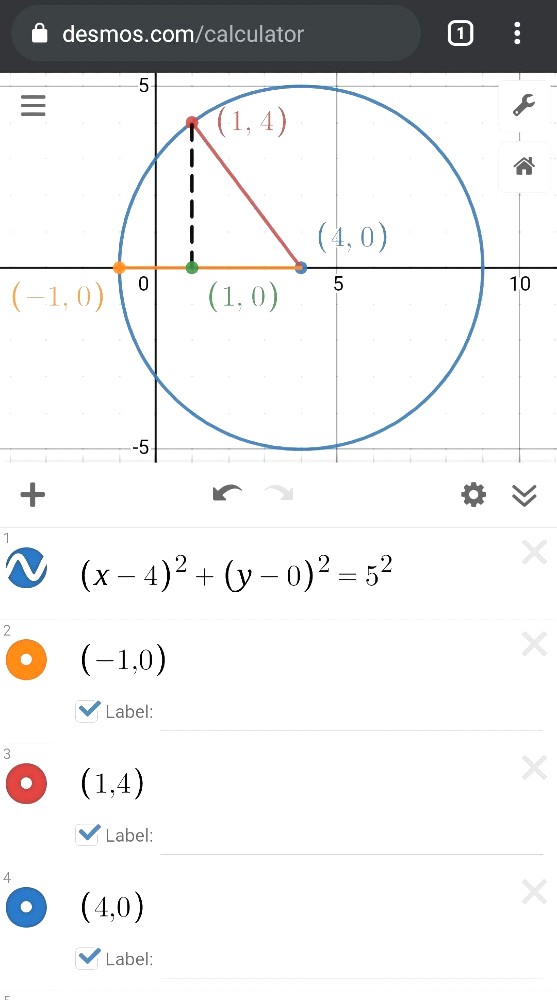
The circle passes through the points (-1,0) and (1, 4) with the y-coordinate of the centre is 0. Find the equation of the circle satisfying this condition. Leave your answers in the standard form.
B (1, 4)
y coordinate of centre is 0
C (x, 0)
Any straight line drawn from the centre of the circle to a random point along the circumference of a circle is called the radius of the circle. A circle will always a fixed radius everywhere (unlike ovals, called ellipses, which can have varying radii).
In short, the lengths AC and BC are two such radii of the circle she must have the same length.
Length of AC
= sqrt of [(x + 1)^2 + (0 - 0)^2]
= sqrt of (x + 1)^2
Length of BC
= sqrt of [(x - 1)^2 + (0 - 4)^2]
= sqrt of [(x - 1)^2 + 16
Both have the same value, so equating lengths AC and BC together,
AC = BC
Squaring both sides eliminates the square roots present.
(x + 1)^2 = (x - 1)^2 + 16
x^2 + 2x + 1 = x^2 - 2x + 1 + 16
2x + 1 = -2x + 1 + 16
2x + 2x = 1 + 16 - 1
4x = 16
x = 4
Then the centre of the circle is (4, 0).
Putting this back into AC, we find that the radius of the circle is 5 units, so the equation of the circle can be represented in standard form as
(x - 4)^2 + y^2 = 25
The √ formula used is the formula for the distance between any two points with on the 2-dimensional Cartesian coordinate system.
For two points with coordinates (a,b) and (x,y) ,
Linear distance (or straight line length) between them
= √[(x - a)² + (y - b)²]
This is actually based on Pythagoras' Theorem.
If you need explanation on the distance formula, let me know.
The subscript c (꜀) stands for 'circle'
The y-coordinate is 0 (given by the question)
The x-coordinate (x꜀) is unknown for now.
We know that the circle passes through the points (-1,0) and (1,4)
So these points lie on the circle's circumference.
Which means that the distance from each point to the centre is the radius.
The radius is the same no matter which point on the circumference you use. (That is also how the shape of the circle is derived. Remember how a circle is drawn using a compass. The distance between the pencil tip and the compass's sharp edge is fixed)
So we use the distance formula to find the radius from each point to the centre.
Since the radius is constant, we equate both expressions.
Substitute the pairs (-1,0) and (x꜀ , 0) into the distance formula on the left hand side. Do the same for (1,4) and (x꜀, 0) on the right hand side (RHS)
(Note that order of sides doesn't matter)
That is how we get :
√[(x꜀ - (-1))² + (0 - 0)²] = √[(x꜀ - 1)² + (0 - 4)²]
√[(x꜀ + 1)² + 0²] = √[x꜀² - 2x꜀ + 1 + (-4)²]
√[x꜀² + 2x꜀ + 1] = √[x꜀² - 2x꜀ + 1 + 16]
We can remove √ from both sides (it's actually squaring both sides, but the mental shortcut is simply to remove it)
x꜀² + 2x꜀ + 1 = x꜀² - 2x꜀ + 1 + 16
Cancelling like terms on both sides, (or you may call it 'bringing over', depending how on you learnt it)
We get :
4x꜀ = 16
x꜀ = 16/4 = 4
So the centre has coordinates (4,0)
What the answer key has provided is a brief summary of the ideas and key steps. It actually skips a lot of steps which may be the reason why you might not see the link.
Next,
Radius of circle is simply :
√[4² + 2(4) + 1] units = √[16 + 8 + 1] units = √25 = 5 units
(If you substitute x꜀ = 4 into the LHS)
Or
√[4² - 2(4) + 1 + 16] units = √[16 - 8 + 17] units = √25 units = 5 units
(If you substitute into the RHS)
Equation of circle in standard form :
(x - a)² + (y - b)² = r², where (a,b) are the centre's coordinates, and r is the radius
So,
(x - 4)² + (y - 0)² = 5²
(x - 4)² + y² = 25
(Note that this is also based on the Pythagoras' Theorem)
Teaching the how , but not the why.
Students just memorise formulas and apply them without being able to appreciate the logic and ideas behind them.
This way, the learning is not conceptual and we see many struggle with such questions.
Same goes for differentiation/integration formulas (understanding of limits is paramount to the mastery) , midpoint formula, section formula, matrices, trigo, sum of interior angles of a polygon, etc.
Even in primary school, area of circle and triangle formulas (obtuse, right angled, or acute) are not explained. Especially for obtuse ones)
See 1 Answer