If 1.4 kg is moved from sack P to sack Q, the masses are the same

Suppose this happens. At the end, sack P and sack Q will have the same value for the mass. Let’s call this value “this value”.

Before this happened, sack P would have 1.4 kg more than “this value” while sack Q will have 1.4 kg less than “this value”. You will need this for the next statement.

——————————

If 1.4 kg is moved from sack Q to sack P, the mass ratio Q to P is 2 : 3.

At this point of time, sack P had 1.4 kg more than “this value” while sack Q had 1.4 kg less than “this value” (the transfer from P to Q has not happened yet)

Now, if the transfer from Q to P proceeds, sack P will have another 1.4 kg extra (and will therefore be 2.8 kg more than “this value”), while sack Q will have another 1.4 kg less (and will therefore be 2.8 kg less than “this value”).

——————————

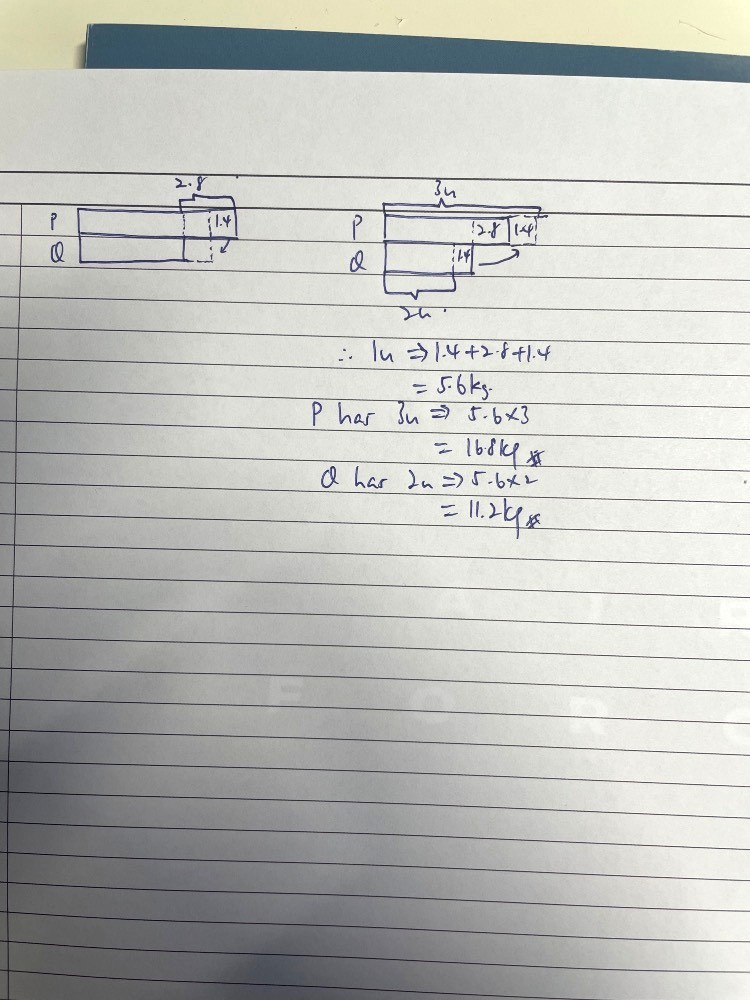
I am typing here and I cannot draw model out obviously, but if you were to draw the model, you will realise that at the end of the transfer from Q to P, P would have 5.6 kg more than Q.

Coincidentally, the ratio of Q to P in this instance is 2 : 3. So, the 5.6 kg would correspond to the extra 1 unit.

1 unit = 5.6 kg
2 units = 11.2 kg (how much Q would have after the transfer from Q to P)
3 units = 16.8 kg (how much P would have after the same transfer)

This transfer does not actually happen, so Q has 11.2 kg + 1.4 kg = 12.6 kg and P has 16.8 kg - 1.4 kg = 15.4 kg.

[Check that if P transfers 1.4 kg to Q, both would have the same quantity of 14.0 kg]

The model would be tough to draw here.

But if you notice clearly, this is what possibly happens.

Let’s change the story to allow Q to have the same quantity of rice as P. At this point, Q has the same number of units as P.

Then, to reach the “start of the original story”, Q must have transferred 1 unit to P, so Q loses 1 unit AND P gains 1 unit. And to reach the “second part of the original story”, Q must have transferred another 1 unit to P, so Q loses another unit AND P gains another unit.

So, Q now has 4 units less than P.

You should convert 2 : 3 to 8 : 12 to reflect this 4 units difference.

This means that the starting ratio must have been 9 : 11.