Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
Secondary 1 | Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

I keep getting a decimal ://
42 = 2 × 3 × 7
63 = 3² × 7
108 = 2² × 3³
Fraction of flowers that are yellow
= 1 - ⅛ - ⅔ - 1/12
= 1 - 3/24 - 16/24 - 2/24
= 3/24
= ⅛
So this means that :
The number of flowers can be divided by 12 and 8 such that we can get whole numbers for the different types of flowers.
This number is also a common multiple of 12 and 8.
(We don't need to consider division by 3, since divisible by 12 already implies that)
Now,
12 = 2² × 3
8 = 2³
So all we have left to do is to find the LCM of 8,12,42,63 and 108.
LCM = 2³ × 3³ × 7
= 8 × 27 × 7
= 1512
So minimum number of flowers altogether
= 1512
Minimum number of yellow flowers
=1512 × ⅛
= 8 × 27 × 7 × ⅛
= 27 × 7
= 189
See 2 Answers



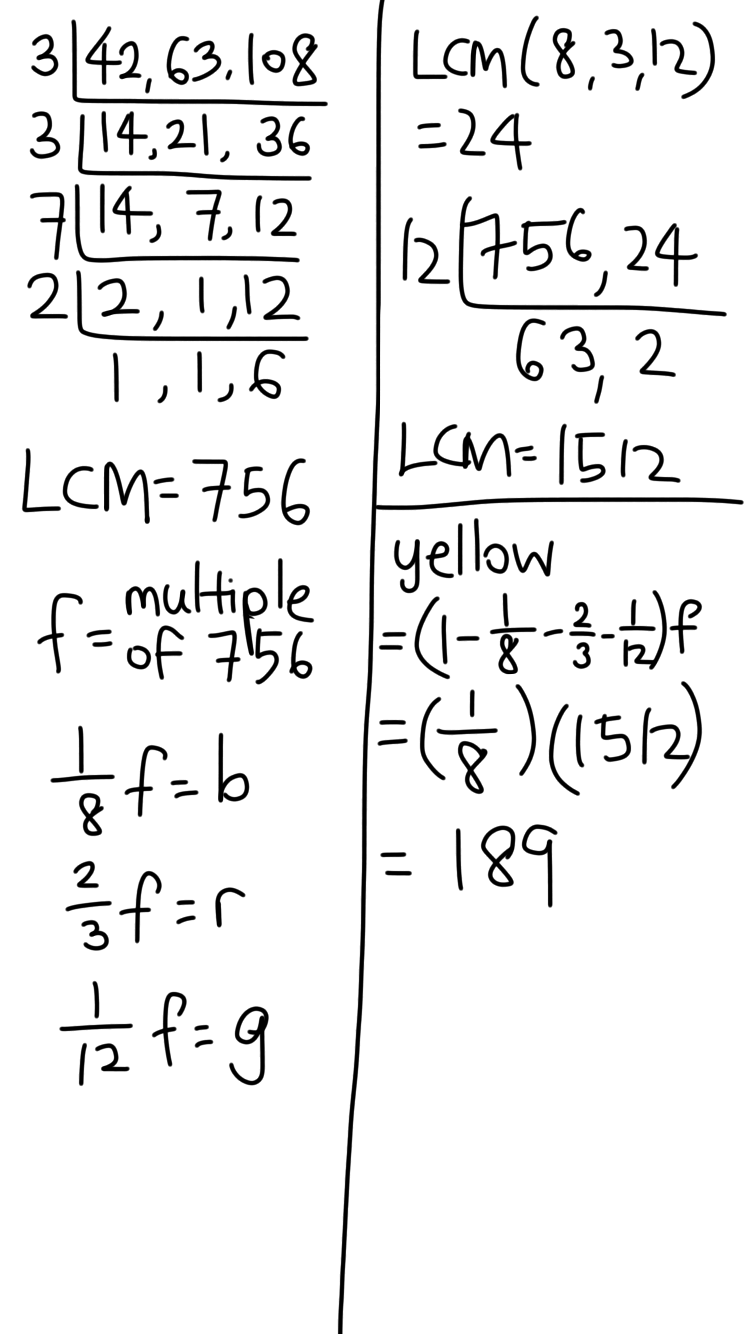


This means that it is a common multiple of all 5 of those numbers.
Since the minimum number of yellow flowers implies the minimum of total number of flowers possible,
Finding the LCM of these 5 numbers would give you your required minimum total number of flowers.
Recall that LCM is Lowest Common Multiple.
He then found the LCM of 3,8,12.
He then took these two results and found their LCM.
The final result 1512 is a number , which is the lowest possible one that is divisible by all 6 numbers.
He did it in 3 separate steps while mine was a combination of all 3. I basically found the LCM of the 5 numbers straight away.
I didn't have to add 3 inside when I do the LCM since 4 out of the 5 numbers contained prime factor 3. This implies my LCM would have at least one factor 3 inside.